Robin

ALU: Implementing shifts with multiplications

Often when cpu instruction sets lack a direct multiplication operation, people resort to implementing multiplication by using combinations of shift and add instructions. Even when a multiplication instruction is available, multiplication by simple powers of two might be faster when performed in a single shift operation that is executed in a single clock cycle than with a multiplication instruction that may take many cycles.

Implementing a shift instruction that can shift a 32 bit register by an arbitrary number of bits can consume a lot of resources though. On a the Lattice up5k i found that it could easily use hundreds of LUTs. (The exact number depends on various things other than register size because placement by next-pnr has some randomness and some additional LUTs might be consumed to meet fan-out and timing requirements, so a design size might change considerably even when changing just a few bits. The multiplexers alone already will consume 160 LUTs)

Turning things around

The up5k on the iCEbreaker board does have something the iCEstick hx1k didn't have: dsp cores, i.e. fast multipliers (at 12Mhz they operate in less than a clock cycle). In fact the up5k has eight dsp cores so i already implemented 32 x 32 bit multiplication using 4 of those, but I still want to have variable shift instructions because they might be needed in all sorts of bit twiddling operations used when implementing a soft floating point library for example.

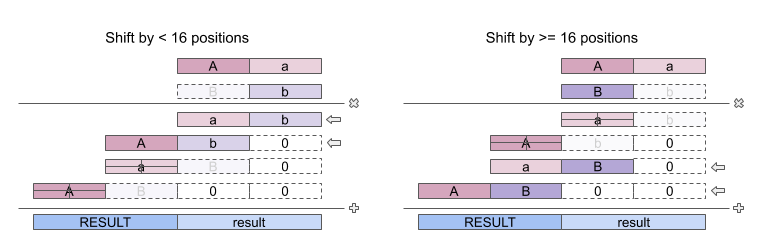
The fun bit is that we can reuse the multiplication units here if we convert the variable shift amount into a power of two. Because calculating the power of two is simply setting a single bit in an otherwise empty register, this takes far less resources.

The verilog code for this part of the ALU is shown below (ALU code on GitHub)

// first part: calculate a power of two
wire shiftq    = op[4:0] == 12;         // true if operation is shift left
wire shiftlo   = shiftq & ~b[4];    // true if shifting < 16 bits
wire shifthi   = shiftq &  b[4];    // true if shifting >= 16 bits

// determine power of two
wire shiftla0  = b[3:0]  == 4'd0;   // 2^0 = 1
wire shiftla1  = b[3:0]  == 4'd1;   // 2^1 = 2
wire shiftla2  = b[3:0]  == 4'd2;   // 2^2 = 3
wire shiftla3  = b[3:0]  == 4'd3;   // ... etc 
...
wire shiftla15 = b[3:0]  == 4'd15;

// combine into 16 bit word
wire [15:0] shiftla16 = {shiftla15,shiftla14,shiftla13,shiftla12,
                         shiftla11,shiftla10,shiftla9 ,shiftla8 ,
                         shiftla7 ,shiftla6 ,shiftla5 ,shiftla4 ,
                         shiftla3 ,shiftla2 ,shiftla1 ,shiftla0};

// second part: reusing the multiplication code
// 4 16x16 bit partial multiplications
// the multiplier is either the b operand or a power of two for a shift
// note that b[31:16] for shift operations [31-0] is always zero
// so when shiftlo is true al_bh and ah_bh still result in zero
// the same is not true the other way around hence the extra shiftq check
// note that the behavior is undefined for shifts > 31

wire [31:0] mult_al_bl = a[15: 0] * (shiftlo ? shiftla16 : shiftq ? 16'b0 : b[15: 0]);
wire [31:0] mult_al_bh = a[15: 0] * (shifthi ? shiftla16 : b[31:16]);
wire [31:0] mult_ah_bl = a[31:16] * (shiftlo ? shiftla16 : shiftq ? 16'b0 : b[15: 0]);
wire [31:0] mult_ah_bh = a[31:16] * (shifthi ? shiftla16 : b[31:16]);

// combine the intermediate results into a 64 bit result
wire [63:0] mult64 = {32'b0,mult_al_bl} + {16'b0,mult_al_bh,16'b0}
                   + {16'b0,mult_ah_bl,16'b0} + {mult_ah_bh,32'b0};

// final part: compute the result of the whole ALU
wire [32:0] result;

assign result = 
            op[4:0] == 0 ? add :
            op[4:0] == 1 ? adc :
            ...
            shiftq ? {1'b0, mult64[31:0]} :
            ...
            ;

The first half constructs rather than computes the power of two by creating a single 16 bit word with just a single bit set. The second half selects the proper multiplier parts based on the instruction (regular multiplication or shift left). The final part is about returning the result: it will be in the lower 32 bits of the combined results. Note that shifting by 32 bits should return zero but selecting for this explicit situation will add more LUTs to my design than I have currently available (using 5181 out of 5280). So for this implementation the behavior for shifts outside the range [0-31] is not defined.

Implementation notes

The code is simple because we do not need all multiplication and addition steps of a full 32 x 32 bit multiplication because if a number is a power of two, only one of the two 16 bits of the multiplier will be non zero (for shift amounts < 32).

Multiplying two 32 bit numbers involves four 16 bit multiplications (of each combination of the 16 bit halves of the multiplier and multiplicand). The four intermediate 32 bit results are then added to a 64 bit result.

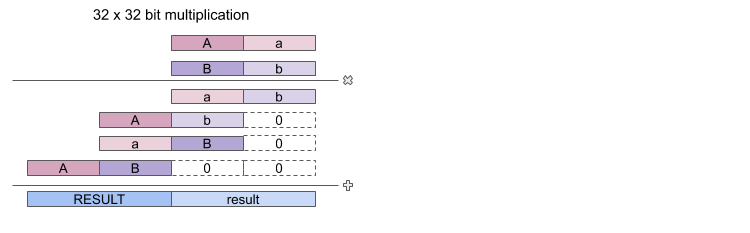
If one of the halves of the multiplier is zero then two multiplication steps are no longer necessary as their result will be zero and the corresponding addition steps will be redundant too.

LUT Usage

Just to give some idea about the resources used by a barrel shifter vs. this multiplication based implementation I have created bare bone implementations (shiftleft.v and shiftleft2.v) and checked those with yosys/next-pnr.

	shiftleft.v (barrel)	shiftleft2.v (multiplier)
ICESTORM_LC	199	67
ICESTORM_DSP	0	3

(side note: the stand alone multiplier implementation only uses 3 DSPs compared to the 4 used by the full ALU but that is because yosys optimizes away the multiplication of both upper halves of the words as they can only end up in the upper 32 bits of the result which we do not use for the left shift)

Right shifts

With left shift available we can now also implement right shift because for a 32 bit register, right shift by N positions can be interpreted as a left shift by 32 - N positions and than looking at the upper 32 bits. This is visualized below

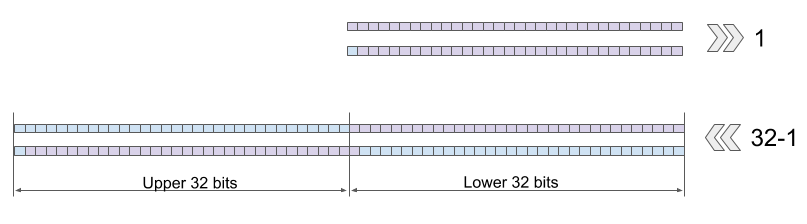
The verilog code needs to be changed only a little bit:

wire shiftq    = op[4:0] == 12;  // true if operation is shift left
wire shiftqr   = op[4:0] == 13;  // true if operation is shift right
wire doshift   = shiftq | shiftqr;
wire [5:0] invertshift = 6'd32 - {1'b0,b[4:0]};
wire [4:0] nshift = shiftqr ? invertshift[4:0] : b[4:0];
wire shiftlo   = doshift & ~nshift[4]; // true if shifting < 16 bits
wire shifthi   = doshift &  nshift[4]; // true if shifting >= 16 bits

...

// 4 16x16 bit partial multiplications
// the multiplier is either the b operand or a power of two for a shift
// note that b[31:16] for shift operations [31-0] is always zero
// so when shiftlo is true al_bh and ah_bh still result in zero
// the same is not true the other way around hence the extra shiftq check
// note that the behavior is undefined for shifts > 31
wire [31:0] mult_al_bl = a[15: 0] * (shiftlo ? shiftla16 : doshift ? 16'b0 : b[15: 0]);
wire [31:0] mult_al_bh = a[15: 0] * (shifthi ? shiftla16 : b[31:16]);
wire [31:0] mult_ah_bl = a[31:16] * (shiftlo ? shiftla16 : doshift ? 16'b0 : b[15: 0]);
wire [31:0] mult_ah_bh = a[31:16] * (shifthi ? shiftla16 : b[31:16]);

...

assign result = 
     ...
     shiftq  ? {1'b0, mult64[31:0]} :
     shiftqr ? {1'b0, mult64[63:32]} :
     ...
     ;

The only thing we do here is subtracting the number of positions to shift from 32 if we are dealing with a shift right instruction and also swap in the correct arguments for the multiplication for both the left and the right shift operation. Also, when selecting the final result we take care of selecting the uppermost 32 bits fro the right shift where a left shift would select the lower 32 bits.